Core Data Engineering: DAGs

🚀 Did you know that Directed Acyclic Graphs (DAGs) have several properties that make them well-suited for data flow programming and scheduling tasks that involve dependencies? If you work with data, understanding DAGs can be a game-changer. Here's why:

• Follow Daniel Palma for more content like this!

🔍 In a graph, edges have a specific direction, which means that each edge in a directed graph is associated with a starting vertex and an ending vertex. This makes it possible to represent relationships or dependencies between vertices that are not symmetrical.

🌀 Acyclic: Directed acyclic graphs (DAGs) do not contain cycles, meaning they can represent tasks or data flows without circular dependencies. DAGs are especially useful for scheduling tasks, ensuring they're executed in the correct order, and avoiding circular dependencies.

👬 Relationships: In a directed acyclic graph (DAG), dependencies between tasks or data flows are represented as edges in the graph, with the direction of the edge indicating the direction of the dependency. This makes it easy to see the relationships between tasks and to understand how they fit together in the overall flow of the program or schedule.

🛣️ Parallelism: Directed Acyclic Graphs (DAGs) are capable of representing parallelism. Since DAGs are cycle-free, it is possible to identify tasks that can be executed in parallel with each other. This significantly improves the efficiency of the program or schedule.

🧙 Topological sorting: A topological sort is an algorithm that takes a DAG as input and produces a linear ordering of the vertices in the graph. This allows for the efficient determination of the order in which tasks or data flows should be executed in a DAG.

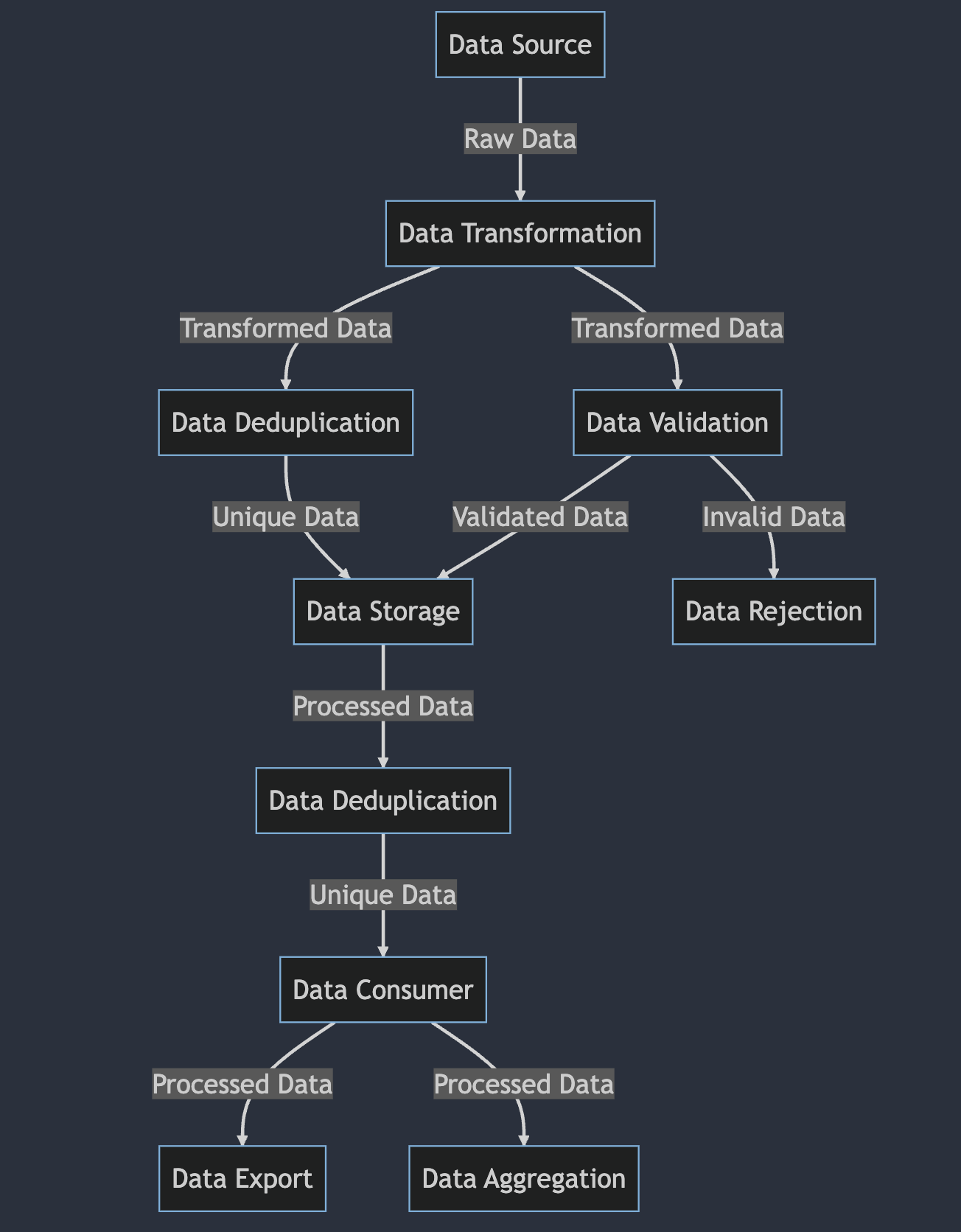
📸 Transitive reduction: Transitive reduction of DAGs is the process of removing certain edges from the graph while still maintaining a DAG and retaining the same transitive closure as the original graph, but with the minimum number of edges. This makes it easier to reason about dependencies in a DAG.

❗ If you're interested in data flow programming or scheduling tasks with dependencies, DAGs are a must-know topic. Understanding the properties of DAGs can help you design and optimize data pipelines and workflows. Do you use DAGs in your work? Let us know in the comments!

#dataengineering #DAGs #dataflows #data #tech #airflow #prefect #dagster